237 words
1 minutes
MD Notes 2 - Distribution of Carriers
Distribution of Carriers
Distribution of electrons at certain energy , is the product of state density of that energy , and the possibility that the energy level is filled by electrons .
(spacial) Density of electrons is the integral of
- : the effective density of states in the conduction band, integral of .
- : degenerately doped n-type semiconductor, where .
- : degenerately doped p-type.
Similarly,
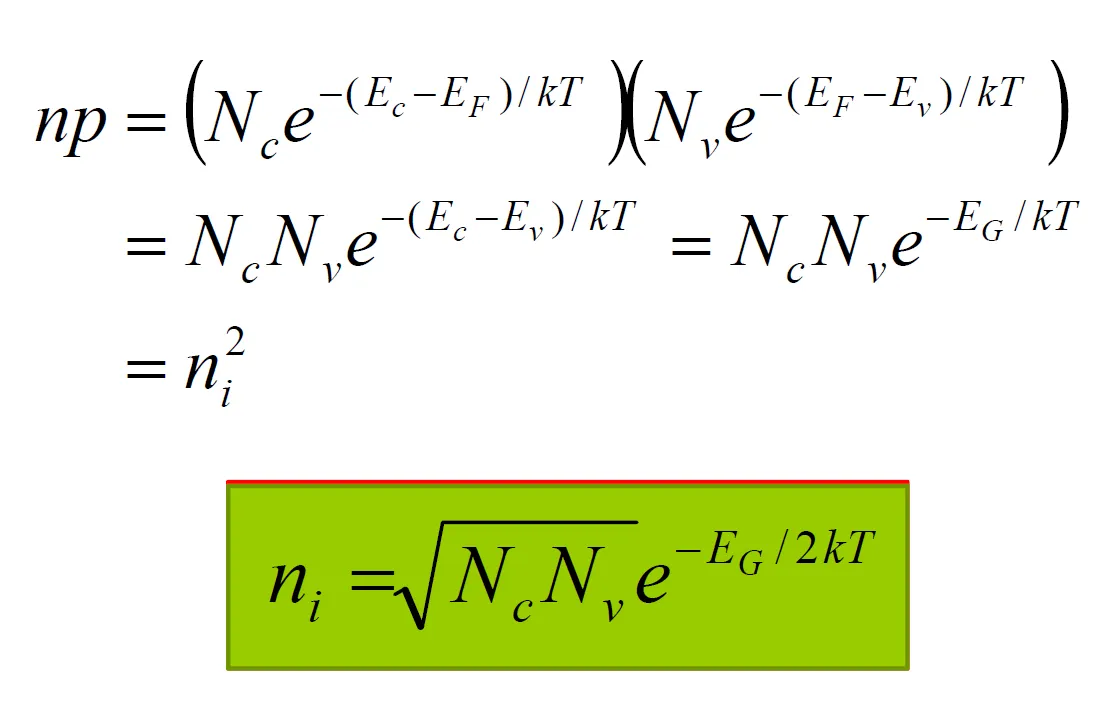
Derive from :
Intrinsic Fermi Level
Using the fact that in intrinsic semiconductor:
is the intrinsic Fermi level.
Also, given that
So carrier concentration could be written as a function of and :
Band Gap Narrowing
If the dopant concentration is a significant fraction of the silicon atomic density, the energy-band structure is perturbed, and the band gap is reduced by .
Dopant Ionization
- Dopant compensation: the effect of one type of dopant is completely or partially cancelled by adding dopant of the opposite type.
- Net dopant concentration: the difference between the concentration of donor and acceptor dopant.
At extreme high temperature, the intrinsic excitation dominates,
MD Notes 2 - Distribution of Carriers
http://tsaoo.github.io/resrvplot/posts/microelectronic-devices/week3-distribution-of-carriers/distribution-of-carriers/ 
