Carrier Actions in Semiconductor

Carrier Actions in Semiconductor#

Drift: charged particle motion under the influence of an electric field.
Diffusion: particle motion due to concentration gradient or temperature gradient.
Recombination-generation:

Thermal Motion#

$\bar{E_k} = \frac{3}{2}kT=\frac{1}{2} m_n^* v_{th}^2$

where $v_{th}$ denotes the thermal velocity (~$10^7$ cm/s at 300K).

Scattering#

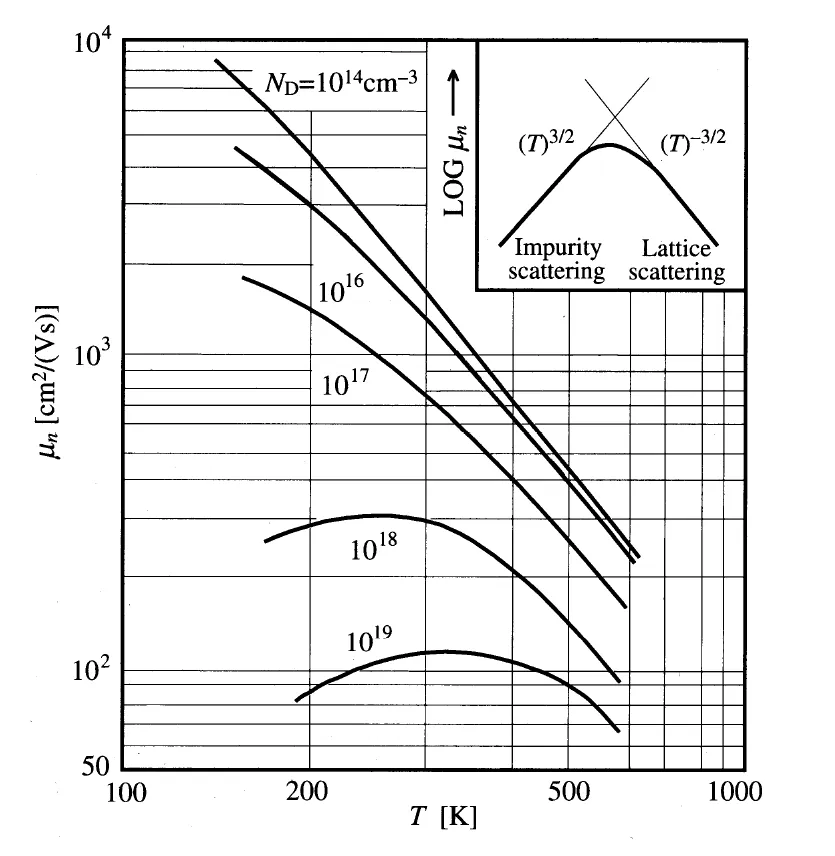
Phonon Scattering: due to collision with vibrating lattice, increases with elevated temp.
Impurity Scattering: due to deflection caused by ionized impurity atoms, decreases with elevated temp.
Charge-charge Scattering: due to deflection caused by Coulomb force between carriers, decreases with elevated temp.

Mean Free Time#

The lose of momentum in every collision equals to the increase of momentum between collisions:

$m_n^* v_d = -qE\tau_{mn}$

where $\tau_{mn}$ denotes the mean free time, $\tau_{mn}$ ~ 0.1 ps.

Drift#

Carrier Mobility#

A measure of the velocity of carriers under electric field of certain strength. $\mu$ has the dimension of $\rm cm^2/(V\cdot s)$

$\mu_n \equiv \frac{q\tau_{mn}}{m_n^*}$

$v_d=\mu E$

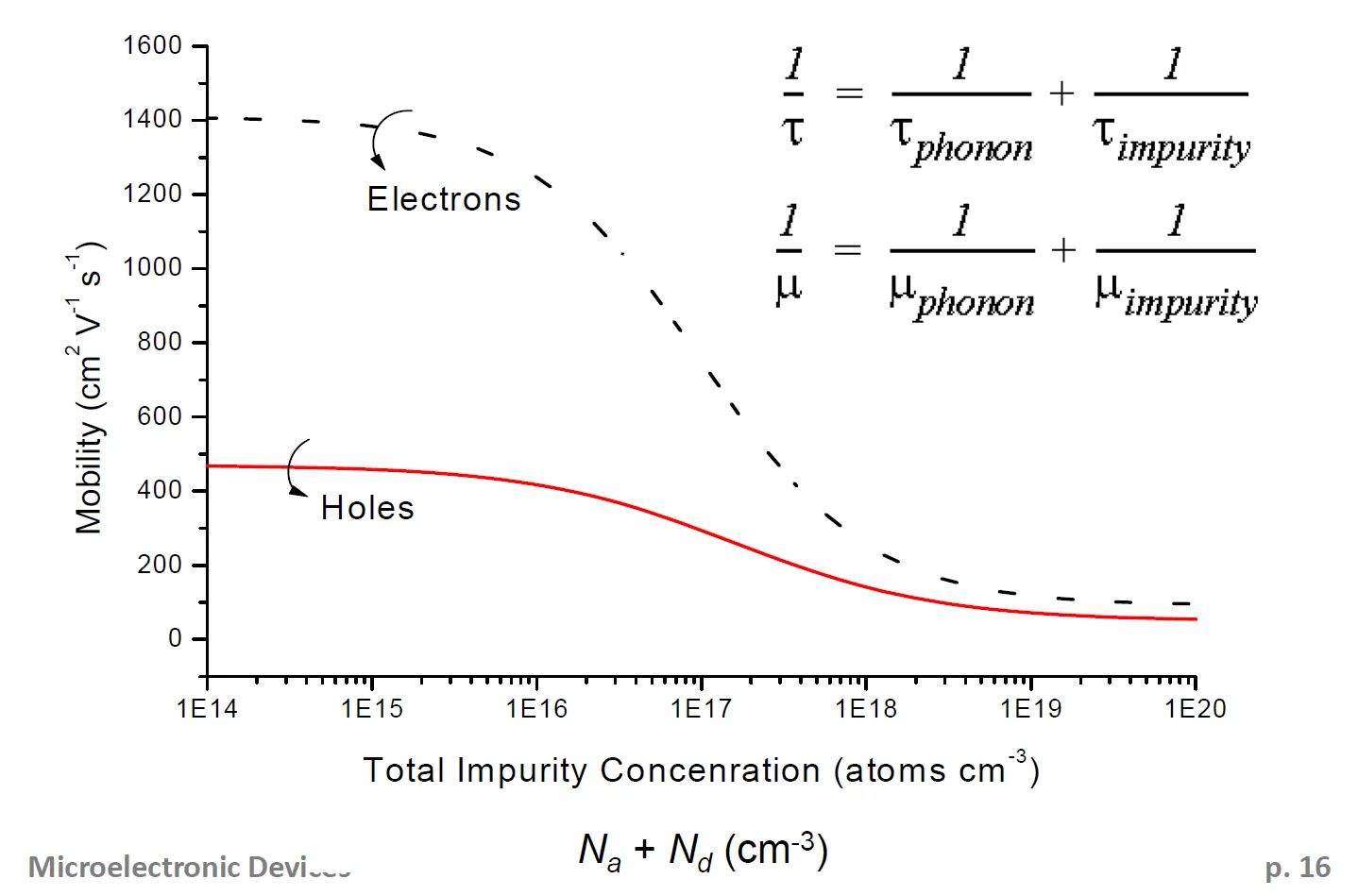
Matthiessen’s Rule: the probability that a carrier will be scattered by mechanism i within a time period ${\rm d}t$ is ${\rm d}t/\tau_i$ , where $\tau_i$ denotes the mean time between scattering events due to mechanism i.

$\frac{1}{\tau_{mn}} = \frac{1}{\tau_{phonon}} + \frac{1}{\tau_{impurity}}$

$\frac{1}{\mu_{mn}} = \frac{1}{\mu_{phonon}} + \frac{1}{\mu_{impurity}}$

Use this chart to get $\mu$ when the total carrier concentration is known.

Use this chart to get $\mu_n$ versus temperature.

Velocity Saturation#

When the kinetic energy of a carrier exceeds a critical value, it generates an optical phonon and loses the kinetic energy. Such phenomenon has a deleterious effect on device speed as in nano-scale transistors.

Drift Current#

$J_{drift} = J_{n,drift} + J_{p,drift} = \sigma E = \left( qn\mu_n + qp\mu_p \right) E$

$\sigma$ denoting conductivity is in S/cm and $\rho$ denoting resistivity is in $\Omega \cdot$cm.

Diffusion#

Carriers diffuse from regions of higher concentration to regions of lower concentration region, due to random thermal motion.

Diffusion Current#

$J_{n,diff} = qD_N\frac{{\rm d}n}{{\rm d}x}$

$J_{p,diff} = -qD_P\frac{{\rm d}p}{{\rm d}x}$

Where $D_N$ and $D_P$ are **diffusion coefficients** of electrons and holes, respectively, with the unit of $\rm cm^2/s$.

The total current, composing $J_{diff}$ and $J_{drift}$ :

$J_n = \sigma E = qn\mu_n E + qD_N\frac{{\rm d}n}{{\rm d}x}$

$J_p = \sigma E = qp\mu_p E - qD_N\frac{{\rm d}n}{{\rm d}x}$

$J = J_n + J_p$

Situation of Thermal Equilibrium#

Under thermal equilibrium, $E_F$ is constant. If the semiconductor is not uniformly doped, then the energy band would vary with position, leading to a built-in electric field, then the drift current and the diffusion current cancels out, resulting in zero net current.

$\frac{{{\rm{d}}n}}{{{\rm{d}}x}} = - \frac{{{N_c}}}{{kT}}{e^{ - \frac{{{E_c} - {E_F}}}{{kT}}}}\frac{{{\rm{d}}{E_c}}}{{{\rm{d}}x}} = - \frac{n}{{kT}}\frac{{{\rm{d}}{E_c}}}{{{\rm{d}}x}} = - \frac{n}{{kT}}q\varepsilon$

So,

$qn\mu_n\varepsilon = qn \frac{qD_N}{kT}\varepsilon$

then

$D_N = \frac{kT}{q}\mu_n$

$D_P = \frac{kT}{q}\mu_p$

namely **Einstein Relationship**, also valid under non-equilibrium conditions ($D_N$ is a constant).

Notice that

$\frac{D}{\mu} = \frac{kT}{q}$

Generation and Recombination (R-G)#

Generation#

Band-to-Band: An electron in valence band gains enough energy (from phonons, etc.) and jumps into the conduction band.
R-G Center: Also called deep-level defects. It lies in the band gap, and may generate a pair of electron-hole.
Impact Ionization: A high-energy electron collides with an atom and knock an additional electron into the conduction band.

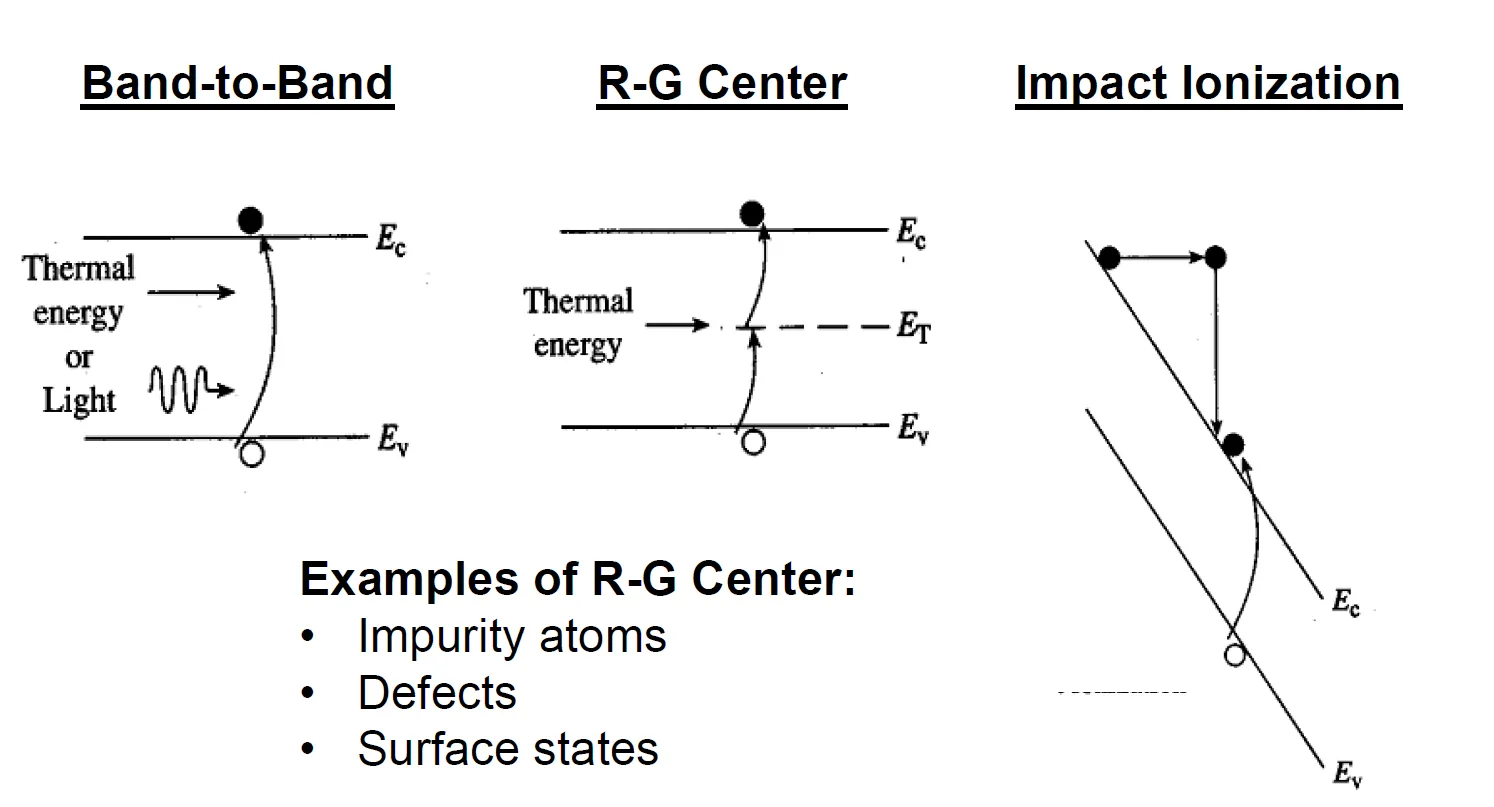
Recombination#

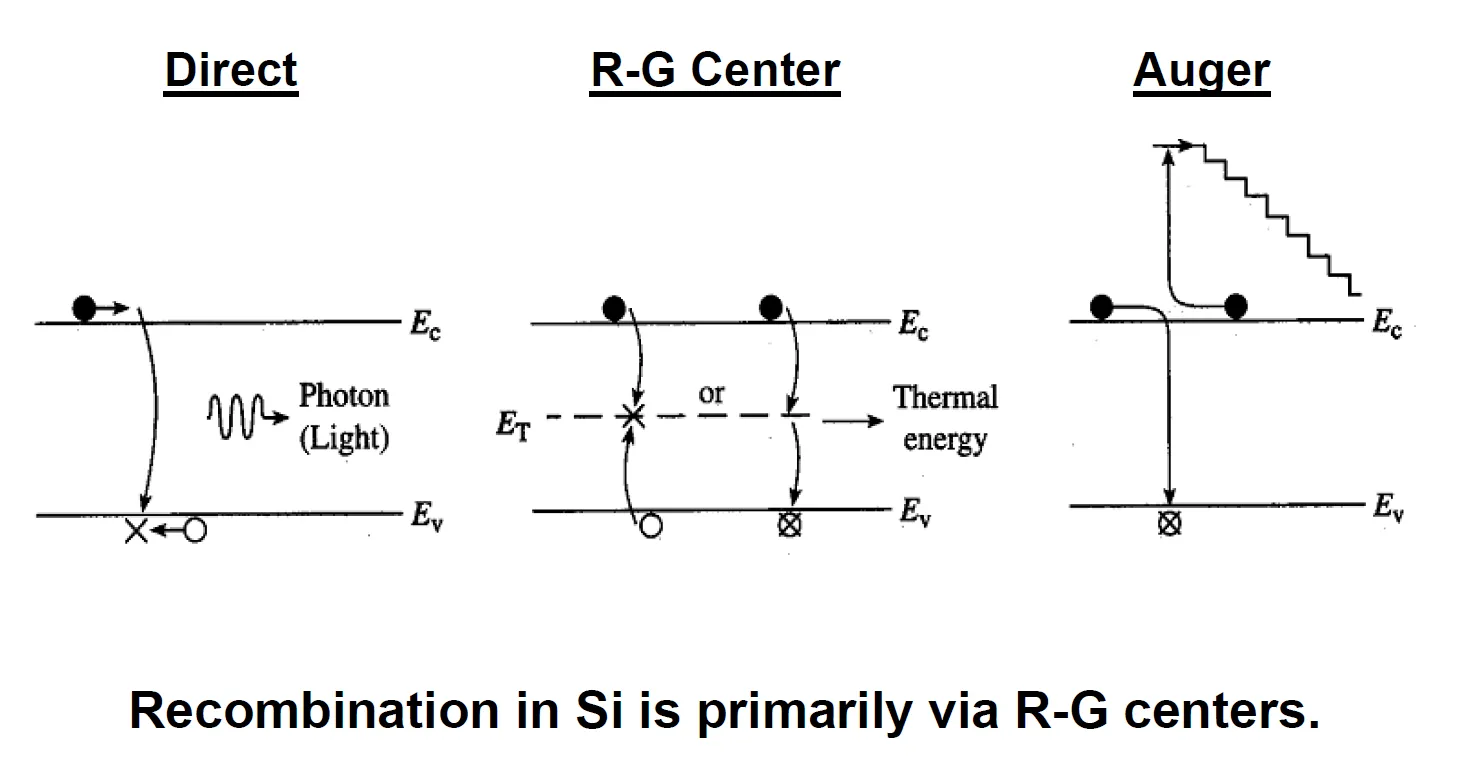
Direct: An electron in conduction band recombines with a hole in valence band, the released energy dissipates as a phonon.
R-G Center (primary): Carriers recombines via defects states in the band gap.
Auger Recombination: Energy released during carrier recombination is transferred to a third carrier, instead of being emitted as a photon.

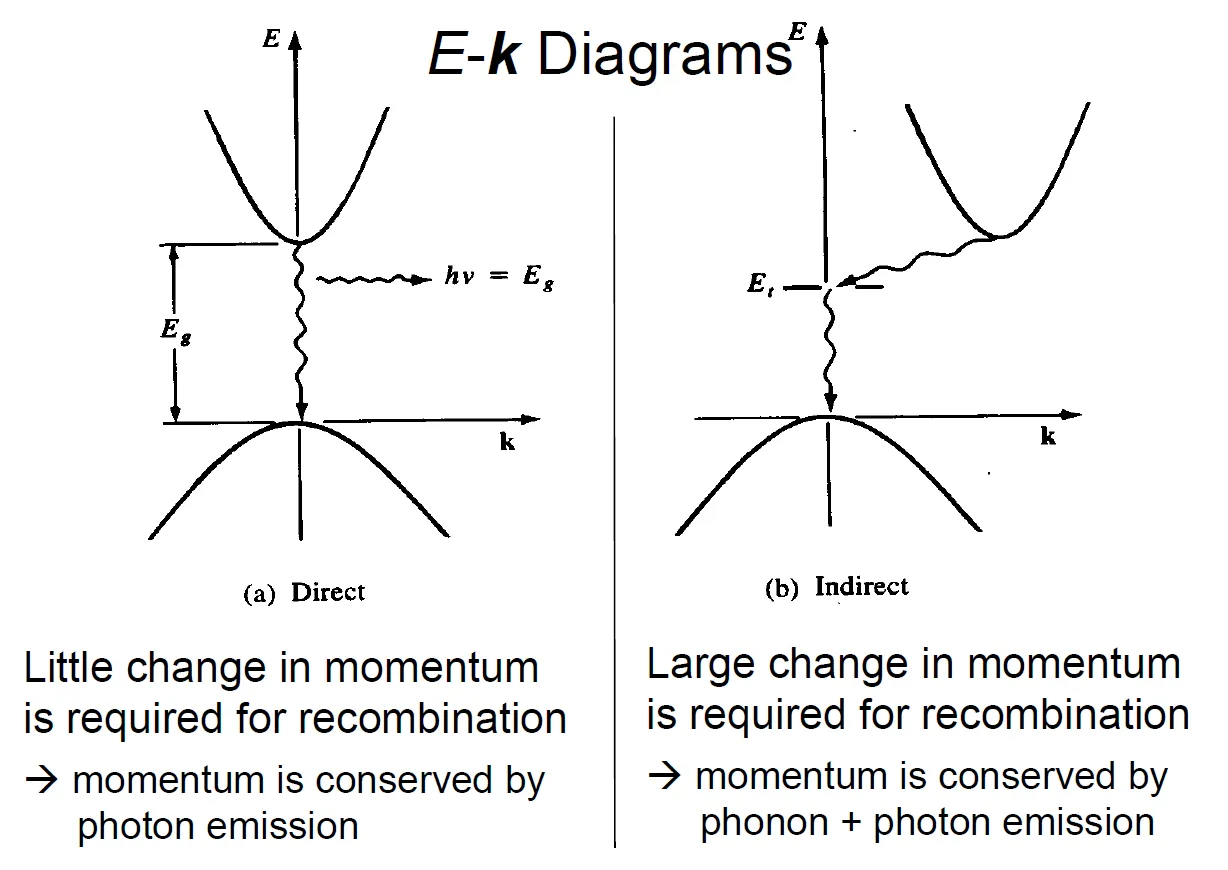
Indirect Band Gap#

alt text